正则表达式实现原理
March 28, 2020
正则表达式引擎可以看作是一个小型的词法分析器,了解它的实现原理不仅可以帮助我们写出更高效的正则表达式,甚至能实现自己定制的文本解析器。
正则表达式
根据 POSIX 规范,正则表达式可以分为基本型(Basic Regular Expression,BRE)和扩展型(Extended Regular Express,ERE)两种,本文讨论的是基本型正则表达式。
正则表达式的语法还是比较复杂的,有时候人都不是很容易去理解一个正则的作用,所以我们需要设计一种机器都能理解的表达方式 —— 有限自动机。有限自动机简单来说是一个识别器,它对每个输入的字符做识别和判断,然后依照规则设定的路径转移到下一个状态。
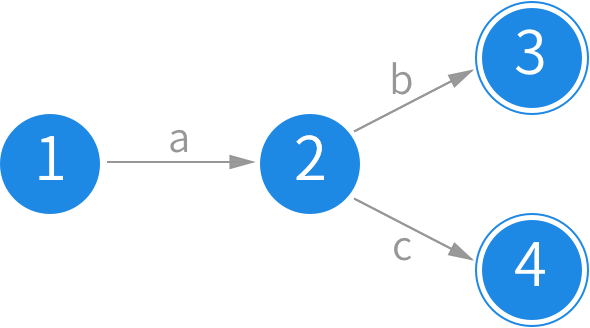
上面是“ab|ac”的状态图。1 是初始状态,输入 a 后就转移到状态 2 上,接着再根据下一个输入字符分别进入状态 3 或状态 4。右边两个圆圈双线的意思是这个状态是可接受的结束状态。一个状态图的结束状态可以是一个或者多个。
有限自动机分为两类:确定性有限自动机(Deterministic Finite Automata,DFA)和不确定性有限自动机(Nondeterministic Finite Automata,NFA)。
有趣的是,所有的正则表达式都能转换成 DFA 或 NFA,同样,所有的 DFA 或 NFA,也都能转换成正则表达式。接下来分别介绍下两者的特点。
DFA 和 NFA
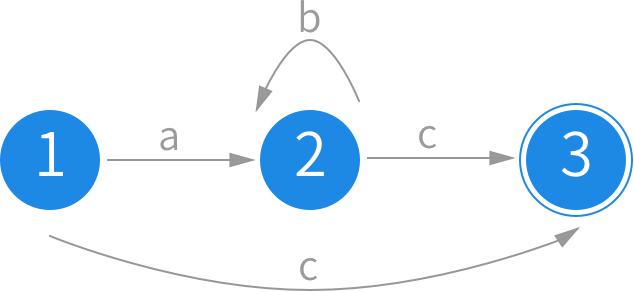
DFA 的特点是,每一个状态都能基于下一个输入的字符进行确定的转换,比如正则表达式 ab*c 的 DFA 状态图如下:
而 NFA 的特点则是,在某些状态的某些输入下,不能做一个确定的转换,这里分成两种情况:
- 同一个输入字符,可以转换到不同的状态。
- 接受空字符 ε,也就是不读入字符就跳转到另一个状态上。
举个例子,正则表达式 a[a-z]*b 要匹配的是,以 a 开头,b 为结尾,中间可以有任意多的小写字符的字符串。对于 aabb 这个字符串,在输入第二个 a 时,将会保持在状态 2 上,但是在输入第一个 b 后,这里就不确定是继续停留在状态 2,还是要转移到状态 3 去了,只有继续输入下一个 b 才能知道刚刚是不应该选择转移的。所以这属于一个 NFA,我们可以构造出下面等价的状态图:
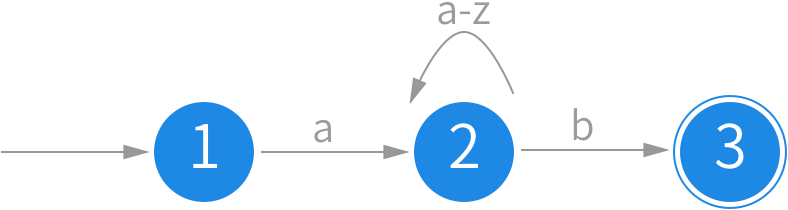
这个 NFA 还有以下这种 ε-NFA 的表示方法,ε 代表的空字符会在连接时去掉,字符串 ab 就是走底下的 ε 路径。

可以看到,NFA 从初始状态开始读取输入的字符串,并使用状态转移函数根据当前状态和刚读取的字符或空串来确定下一个状态。但是 NFA 的下一个状态有可能属于一个状态集合,这个状态集合还依赖于后续的输入才有可能确定唯一所处的状态。如果当自动机完成读取的时候,它处于接受状态的话,则说明 NFA 接受了这个字符串,否则它就是拒绝了这个字符串。
虽然 DFA 比 NFA 简单,但是对于机器来说构造 NFA 要比构造 DFA 更加容易,ε 边的存在也是为了更方便地用下文提到的算法把一个正则表达式转换成 ε-NFA。
从正则表达式生成 ε-NFA
Thompson 构造法通过下面的规则把正则表达式转变为 ε-NFA:
ε 转换
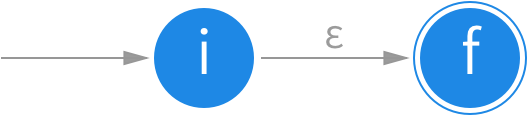
不接受任何输入,就从一个状态转换到另一个状态,状态图的边上标注 ε。
字符转换
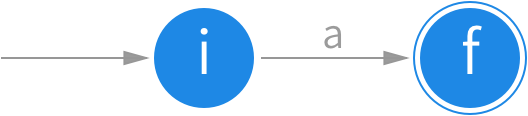
当接受字符 i 的时候,触发一个转换,状态图的边上标注 i。
选择:s|t
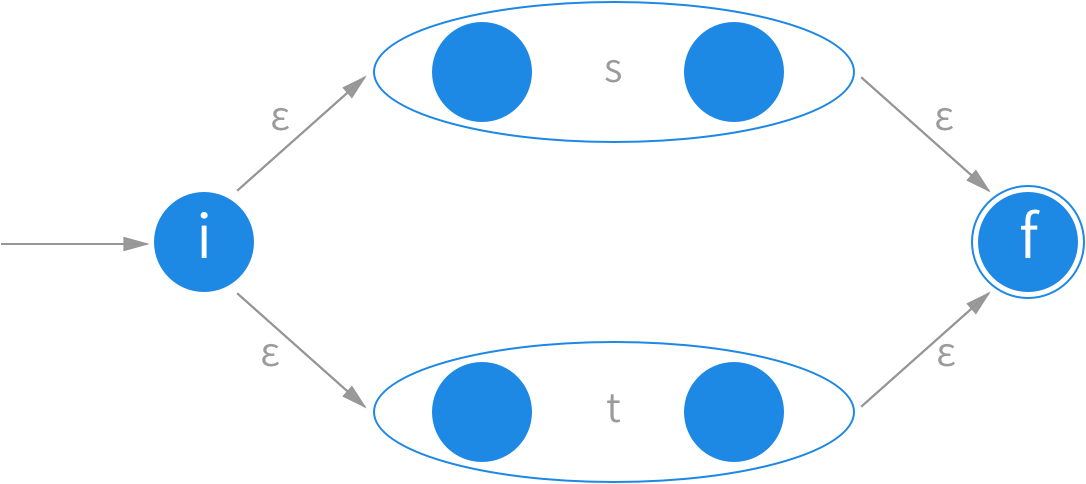
s 和 t 是两个不同的子正则表达式。s|t 的意思是二者选一。这里创建一个新的起始状态 i,并且用 ε 转换连接到所有分支的起始状态上。然后为了表示某个分支最终是可接受的,再把所有分支的结束状态都连接到整个规则的新结束状态 f 上。
连接:st

st 的转换规则是先把 s 的起始状态变成整体的起始状态,接着将 t 的结束状态变成整体的结束状态,最后用 s 的结束状态变成 t 的起始状态。这样两个子正则表达式就连接起来,匹配完了 s 接着匹配 t。
闭包:s*
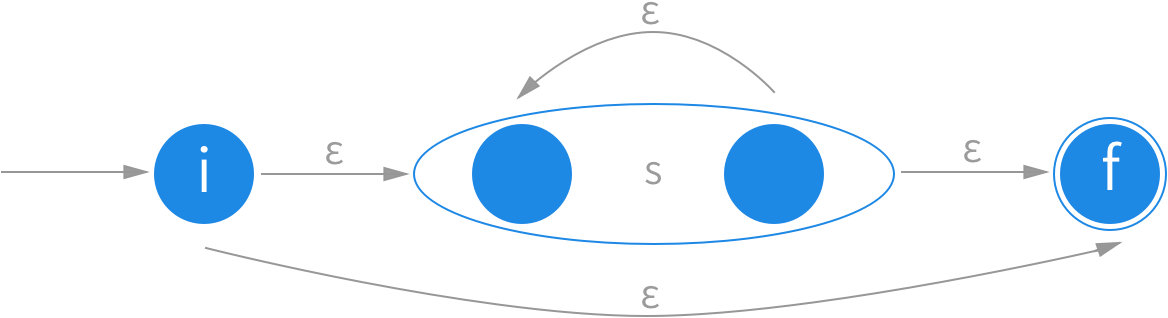
闭包表示的是重复。我们同样为整个规则增加两个新的状态:起始状态 i 和结束状态 f。i 直接到 f,表示匹配了零次。如果遇到一个可以让规则接受的字符,就从 s 的结束状态回到它的起始状态。具体实现差不多是这样的:
static func zeroOrMore(_ trans: inout StateTransition) -> Bool {
if !lexer.match(.zeroOrMore) {
return false
}
// 新增起始和结束状态
let start = State()
let end = State()
// 新的起始状态连接到原来的起始状态和新的结束状态
start.nexts.append(trans.startNode!)
start.nexts.append(end)
// 原来的结束状态连接到自身的开始状态和新的结束状态
trans.endNode?.nexts.append(trans.startNode!)
trans.endNode?.nexts.append(end)
// 替代原来的起始和结束状态
trans.startNode = start
trans.endNode = end
_ = lexer.advance()
return true
}
按照这 5 个规则我们就能把任意的正则表达式转换成一个 ε-NFA 了。但是只得到 ε-NFA 还不行,因为 ε-NFA 存在多条可能的路径,在运行的过程中需要试探和回溯,极大地降低效率。因此,我们还需要一个办法来消除这些非确定性。
把 ε-NFA 转换成 DFA
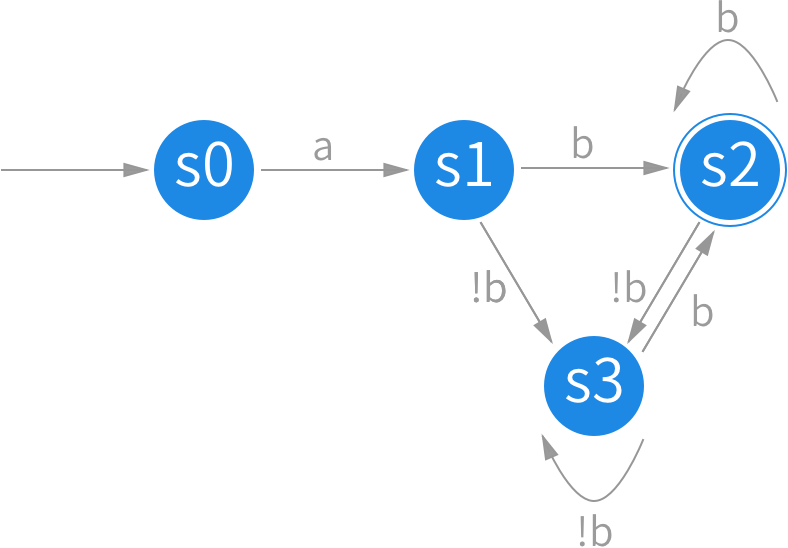
NFA 转 DFA 的方法可以使用子集构造法,算法的关键在于找到 ɛ 闭包,ε-closure(s),状态 s 的 ɛ 闭包为 s 经过任意条 ɛ 边所能达到的状态的集合。构造 DFA 的过程其实就是不断地计算 ɛ 闭包。还是以 a[a-z]*b 作为例子,具体步骤如下:
-
设定初始集合 s0。这里只包含状态 1,即:ε-closure(s0) = {1}
-
计算 s0 集合中的所有状态在输入一个字符时得到的下一个状态集合。move(s0, a) 即从集合 s0 接收字符 a 后得到的新状态集合:s1 = ε-closure(move(s0, a)) = {2, 3, 5}
/// 计算当前状态集在输入一个字符时得到的下一个状态集
func move(_ set: [State], _ c: Character) -> [State] {
var res = [State]()
for state in set where state.edge == c {
for next in state.nexts {
res.append(next)
}
}
return res
}
- 分别计算上一步状态集合的 ɛ 闭包(虽然这个例子上一步只产生 s1 一个结果,不过其他情况也同理)。这里对下一个字符分成
b和!b两类:s2 = ε-closure(move(s1, b)) = {4, 6},s3 = s-closure(move(s1, !b)) = {3}
/// 计算当前状态集的 ε 闭包
func closure(_ set: [State]) -> [State] {
var res = set
var stack = [State]()
for state in set {
stack.append(state)
}
while stack.count > 0 {
let state = stack.removeLast()
if state.edge == Character("ε") {
for next in state.nexts {
res.append(next)
stack.append(next)
}
}
}
return res
}
- 对 s2 和 s3 重复上述操作,直到没有新的集合产生。
按照这个思路,构造出的 DFA 为:
总结
总的来说,一个正则表达式引擎工作流程有如下几步:
-
解析正则表达式进行预处理
-
利用 Tompson 算法转换成 NFA
-
通过子集构造法把 NFA 转为 DFA
-
判断 DFA 是否接受输入串
需要补充的是,转为 DFA 这一步其实不是必须的,因为构造出的 DFA 状态数量可能很大,占用更多的空间,并且生成 DFA 本身也需要消耗计算资源,有些工具就是基于 NFA 而不是 DFA,例如:emacs,grep,vi,所以还要根据实际需求选择采用 NFA 还是 DFA。
最后,一个简单的用 Swift 实现的 NFA 正则表达式引擎可以看这里。